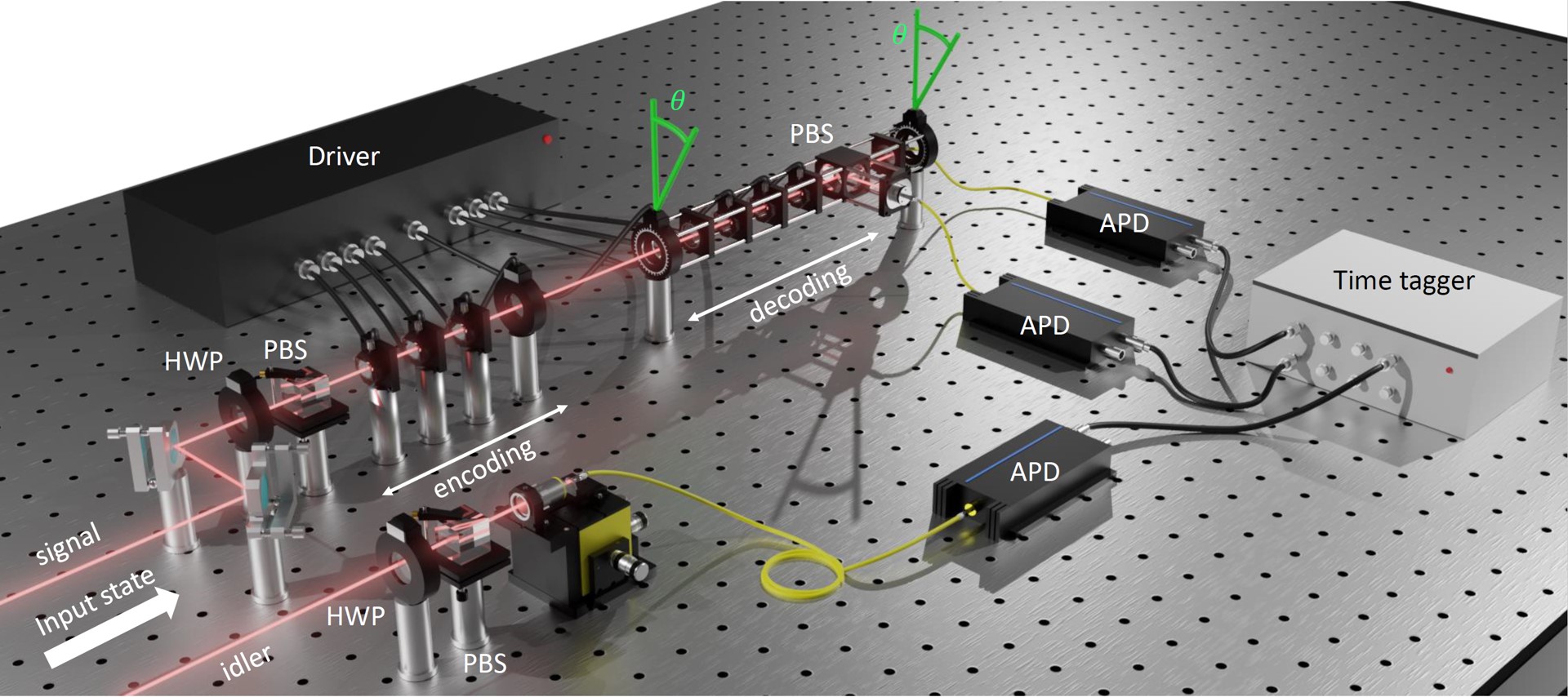
Adopting quantum resources for parameter estimation discloses the possibility to realize quantum sensors operating at a sensitivity beyond the standard quantum limit. Such an approach promises to reach the fundamental Heisenberg scaling as a function of the employed resources N in the estimation process. Although previous experiments demonstrated precision scaling approaching Heisenberg-limited performances, reaching such a regime for a wide range of N remains hard to accomplish. Here, we show a method that suitably allocates the available resources permitting them to reach the same power law of Heisenberg scaling without any prior information on the parameter. We demonstrate experimentally such an advantage in measuring a rotation angle. We quantitatively verify sub-standard quantum limit performances for a considerable range of N (O(30,000)) by using single-photon states with high-order orbital angular momentum, achieving an error reduction, in terms of the obtained variance, >10 dB below the standard quantum limit. Such results can be applied to different scenarios, opening the way to the optimization of resources in quantum sensing.
Experimental metrology beyond the standard quantum limit for a wide resources range