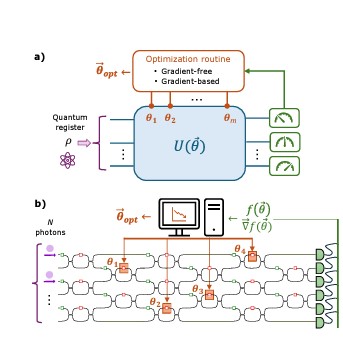
In the current era of noisy intermediate-scale quantum computers, variational quantum algorithms represent one of the most viable approaches for their application to solve tasks of interest. These algorithms train a parameterized quantum circuit to execute a specific task encoded in a cost function that needs to be minimized using a classical optimizer. In this context, photonic platforms based on reconfigurable integrated optics appear as one of the prominent platforms for the implementation of variational algorithms. In the circuital model of quantum computation based on qubits, to train variational circuits, the parameter shift rule came into being, which allows for the exact calculation of the derivatives of many functions at the output of a quantum circuit, opening up the possibility of using classical optimisation algorithms based on gradient descent. In this paper, we derive a formulation of the parameter shift rule for reconfigurable optical linear circuits based on the Boson Sampling paradigm. This allows us to naturally embed the common types of experimental noise, such as partial distinguishability, and mixedness of the states, thus obtaining a resilient approach. We also present similar rules for the computations of integrals over the variational parameters. Finally, we employ the developed approach to experimentally test variational algorithms with single-photon states processed in a reconfigurable 6-mode universal integrated interferometer. Specifically, we apply the photonic parameter shift rules to the variational implementation, on a photonic platform, of both an eigensolver and a Universal-Not gate.
“Variational approach to photonic quantum circuits via the parameter shift rule”