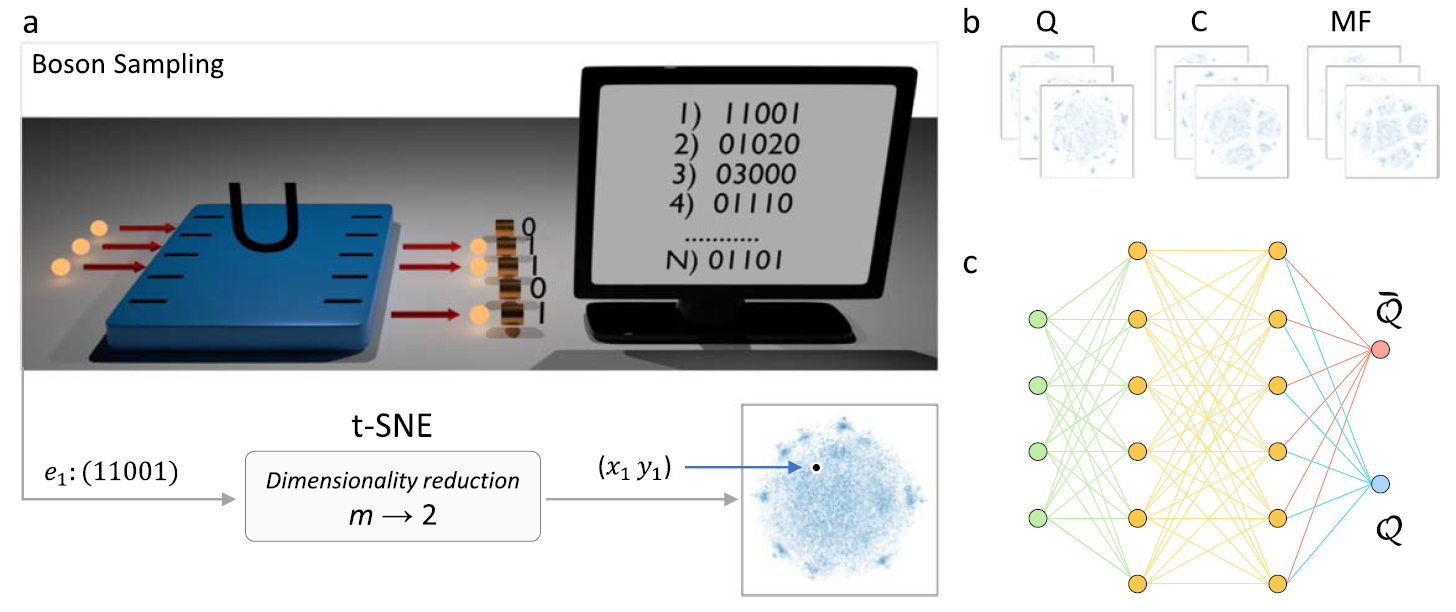
Classical machine learning algorithms can provide insights on high-dimensional processes that are hardly accessible with conventional approaches. As a notable example, t-distributed Stochastic Neighbor Embedding (t-SNE) represents the state of the art for visualization of data sets of large dimensionality. An interesting question is then if this algorithm can provide useful information also in quantum experiments with very large Hilbert spaces. Leveraging these considerations, in this work we apply t-SNE to probe the spatial distribution of n-photon events in m-dimensional Hilbert spaces, showing that its findings can be beneficial for validating genuine quantum interference in boson sampling experiments. In particular, we find that nonlinear dimensionality reduction is capable to capture distinctive features in the spatial distribution of data related to multi-photon states with different evolutions. We envisage that this approach will inspire further theoretical investigations, for instance for a reliable assessment of quantum computational advantage.
Visual assessment of multi-photon interference published in Quantum Science and Technology!